Ir al contenido principal

🎮 El método mas fácil y eficaz para resolver las Ecuaciones exponenciales

Ecuaciones exponenciales 

Una ecuación exponencial es aquella que su incógnita, ya sea x o cualquier otra, aparece en el exponente.
Todo sobre las ecuaciones exponenciales; desde su definición hasta ejercicios desarrollados paso a paso.

Propiedades de la potenciación 

Como las ecuaciones exponenciales conllevan una potencia, es necesario recordar las propiedades de la potencias que nos permite simplificar el proceso y facilita su resolución. Entre las propiedades de las potencias más usadas, se encuentran:


  • Potencias con base cero y uno: Toda expresión elevada a cero, da uno. Toda variable elevada a uno, da el mismo valor elevado. 

Ejercicios de potencias con base cero y uno.

  • Productos de potencia de igual base: La multiplicación de dos o más potencias con la misma base, es igual a la base elevada a la suma de todos los exponentes. Se pone la misma base y se suman los exponentes.

Ejercicios de potencia de igual base desarrollados paso a paso

  • Cocientes de potencias de igual base: La división de dos o más potencias con la misma base, es igual a la base elevada a la resta de todos los exponentes. Se pone la misma base y se resta los exponentes.

Ejercicios de cociente de igual base desarrollados paso a paso

  • Potencia de una potencia: Se coloca la misma base y se multiplica los exponentes.

Ejercicios de potencia de una potencia desarrollados paso a paso

  • Potencia de un producto: Cada base se multiplica por el exponente.

Ejercicios de potencias de un producto desarrollados paso a paso

  • Potencia de una división: Cada base se divide para el exponente.

Ejercicios de potencias de una división desarrollados paso a paso

  • Potencia con exponente negativo: Se coloca en forma de fracción; en el numerador se coloca el número 1 y en el denominador, la misma base pero con exponente positivo.

Ejercicios de potencia con exponente negativo desarrollado paso a paso

Tabla de potencias

Los valores que se encuentran en la prueba son realmente pequeños, es muy raro observar valores de 6 u 8 cifras. En la tabla encontrarás solo las potencias necesarias para la prueba Ser Bachiller: 
Tabla de potencias para resolver las ecuaciones exponenciales de forma más ágil.

Procedimiento, paso a paso 

  • Iguala las bases de todos los exponentes. Si no existe relación entre las bases no podrás pasar al siguiente paso.

El método más eficaz y rapido para resolver las ecuaciones exponenciales para la prueba ser bachiller

  • Desciende los exponentes y sepáralos con un igual.

El método más eficaz y rapido para resolver las ecuaciones exponenciales para la prueba ser bachiller

  • Despeja la x de manera correcta. 

El método más eficaz y rapido para resolver las ecuaciones exponenciales para la prueba ser bachiller

Ejemplos paso a paso 

1. Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen. 
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.


Si es necesario conocer la rapidez de la partícula, ¿Cuál es el tiempo en que la partícula pasa por el sensor? 
Iguala las bases. En este caso, el número correcto es 2.
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.

Desciende los exponentes, recordando las propiedades de la potencias. Como existe una multiplicación de potencias, solo debes sumar.
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.



Multiplica y suma, para obtener una ecuación tipo lineal. Despeja la incógnita o x. 
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.

Trucazo, para resolverlo en menos tiempo


Está es la forma más recomendable para la prueba Ser Bachiller, debido a que no necesitas mucho tiempo para hallar la respuesta o solución, pero necesitas mucha práctica y conocer las propiedades de la potencias, porque es una forma simplificada de resolución.
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.



Fija la base o el número que elevado puedas obtener cada uno de los valores base de la ecuación exponencial.
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.



Multiplica los exponentes de los valores base, por sus respectivos exponentes de la ecuación exponencial. 
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.



Encuentra la solución, despejando la incógnita.
Un grupo de estudiantes realiza un experimento para conocer el movimiento de una partícula atómica y mediante un programa computacional obtiene la función de su trayectoria, donde x es el tiempo, en segundos, en que esta pasa por un sensor ubicado a 16 km del origen.



2. Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación: 
Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:



Donde:Y: El número de artículos.T: El mes que se registran esas ventas.


         ¿En qué mes se vendieron 15625 artículos? 


Escribe los nuevos datos en la ecuación exponencial. Iguala las bases para todos los valores, en este caso, el número 5. 


Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


Descienda los exponentes, recordando las propiedades de la potencia. 


Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


Despeja la incógnita o t. 


Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


Trucazo 

Fija las bases o el número que elevado puedas obtener cada uno de los valores base de la ecuación exponencial. 


Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


Multiplica los exponentes de los valores base, por sus respectivos exponentes de la ecuación exponencial.


Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


Encuentra la solución, despejando la incógnita.


Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:

3. Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación: 

Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:

¿En qué mes se vendieron 3125 artículos? 

Escribe los nuevos datos en la ecuación exponencial. Iguala las bases para todos los valores, en este caso, el número 5.

Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:

Descienda los exponentes, recordando las propiedades de la potencia.  

Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


Despeja la incógnita o t. 

Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


4. Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación: 

Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:


¿En qué mes se vendieron 15625 artículos? 


Escribe los nuevos datos en la ecuación exponencial. Iguala las bases para todos los valores, en este caso, el número 5.

Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:

Descienda los exponentes, recordando las propiedades de la potencia.  

Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:

Despeja la incógnita o t. 
Una empresa de cuadernos experimenta un crecimiento exponencial en sus ventas, después de presentar una campaña publicitaria en redes sociales. La función que representa el número de artículos vendidos en relación al tiempo se puede representar mediante la ecuación:

Etiquetas:

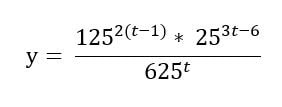
Comentarios

Publicar un comentario

Entradas más populares de este blog

📕 El método infalible para identificar la tesis de un texto

Tesis La  tesis de un texto  es la opinión relativamente corta del autor o autora, demostrándolo o fortaleciendo con argumentos en el desarrollo o cuerpo del mismo. Formas de identificar la tesis de un texto Deberás analizar y encontrar palabras que estén relacionadas con conclusión o afirmación debido que es la forma más común de expresar una opinión. Palabras como “en conclusión, en resultado de, ya que, porque, en consecuencia, por lo tanto, entonces” hacen referencia a una  conclusión . Palabras como “son, es, ciertamente, realmente” hacen referencia a una  afirmación . Ejemplos, paso a paso 1. Con base en el texto, identifique la tesis. Las redes sociales son un excelente instrumento para potenciar distintas formas de enseñanza y aprendizaje. En este sentido, se concebirán las redes como una herramienta de democratización de la información que transforma a las personas en receptores y en productores de contenido. El uso de las redes...
15 comentarios
Leer más

🎮 Regla de tres

Regla de tres  La regla de tres es una operación realmente simple que permite encontrar un determinado valor, a partir de tres variables o números. En la prueba Ser Bachiller este tipo de ejercicios es muy normal, asociados a temas como tiempo, longitud, trabajo, producción, entre otras cosas.  Este tipo de problemas se puede resolver bajo dos métodos, los mismos que aplican para casos muy definidos. Estos son:  Método Quién, Tiempo y Obra Este método solo se utiliza en el caso de tener las variables de quién, tiempo y obra. La mayoría de ejercicios en la prueba Ser Bachiller se puede resolver bajo este modelo.  Para usar correctamente este modelo debes saber que las variables son fijas. Al momento de ordenar los valores del ejercicio debes agruparlos en el orden de: primero quien, luego tiempo y por último, obra.  Multiplica en línea recta entre quién y tiempo, y en cruz, entre tiempo y obra.  Asig...
1 comentario
Leer más

🎮 Descuento y aumento único

Descuento y aumento único El  descuento y aumento único  es simplemente una fórmula que nos permite encontrar el porcentaje verdadero que pierde o conserva una determinada bacteria. En la  prueba Ser Bachiller hasta el año 2018, solo han tomado descuento único, pero es posible que más adelante tomen en cuenta, el aumento único.  Fórmulas   Du:  Descuento único  A 1 :   Primer descuento A 2 :  Segundo descuento Au:  Aumento único A 1 :  Primer descuento   A 2 :  Segundo descuento Ejemplos, paso a paso⭐️ 1.  En el cuerpo humano habitan aproximadamente un millón de bacterias por centímetro cuadrado. Si al tomar un baño se pierde el 20% de estas y, si al usar jabón antibacteriano se pierde un 10% adicional, ¿qué porcentaje de bacterias se pierde y se conserva en el cuerpo?   Intercambia los datos en la fórmula de descuento único. Simplifica las variables posibl...
Publicar un comentario
Leer más